How Mathematics and Physics Look at the Sum of 1 plus 1 or Is de Broglie's Theory Applicable to Macroscopic Objects?

 

How Mathematics and Physics Look at the Sum of 1 plus 1

or

Is de Broglie's Theory Applicable to Macroscopic Objects?

Pavle I. Premović

Laboratory for Geochemistry, Cosmochemistry&Astrochemistry,

University of Niš, pavleipremovic@yahoo.com, Niš, Serbia

Back in elementary school or often in our parents’ home much earlier, we were taught that 1 plus 1 equals 2. No one doubts that elementary mathematical statement. However, from a physicist's point of view, that claim is doubtful. Indeed, in his opinion, in the macroscopic world, 1 + 1 is not 2. One sand grain cannot be simply added to another because they are different. The same can be said for volcanic ash particles, volcanic bombs, asteroids, comets, planets (and their moons), stars and galaxies (hereinafter macroscopic objects).[1]

Let us consider the microscopic world. The simplest atom is the hydrogen atom H. Two of these atoms are identical.[2] The same can be said for two protons or two neutrons and all other microscopic objects. The simplest molecule is the hydrogen molecule. Two of these molecules are also identical. Thus, in contrast to macroscopic objects, microscopic objects can be added to each other. In other words, the microscopic world and elementary mathematics are even in agreement on the elementary level. In our opinion, the macroscopic and microscopic worlds are so distinct that their reconciliation is pointless.

The foundation for modern quantum physics is de Broglie’s theory. This theory states that all matter has a wave-like nature and can be described through his mathematical equation:

λ = h/mv    … (1)

where h (= 6.63×10⁻³⁴J sec) is Planck’s constant, m and υ is the mass and speed of the object.  According to this equation, the Broglie’s theory is even applicable to the moving microscopic particles as well to the moving macroscopic objects.

Heisenberg's Uncertainty Principle is a fundamental principle of quantum physics. It states that it is impossible to know exactly both the position and the momentum of a particle simultaneously. This principle can be only applied to the microscopic particles and arises from their wave-matter duality. The origin of the uncertainty principle is found in the duality of particles in quantum physics.

Quantum physics states a microscopic particle can be in two places at once. As far as we are aware, this was experimentally demonstrated for the electron but also some complex giant molecules. One can extend this conclusion to the macroscopic objects. Indeed, if a galaxy or a group of galaxies can also occupy two places at once then we have two universes at once.

Quantum entanglement is a quantum physical phenomenon that occurs when the microscopic particles photons, electrons, atoms, or molecules interact quantum-mechanically even when they are separated by large distances in space. Of course, the macroscopic objects as listed above cannot interact quantum-mechanically.

New experiments from two separate teams of researchers {1, 2} reported observing quantum entanglement between two aluminum membranes (“drums”), of about 10 micrometers in size. They managed to simultaneously measure the position and the momentum of the two drums. This is possible since, as we stated above, the Heisenberg uncertainty principle is valid only for microscopic particles but not for macroscopic objects. It appears that the size of these drums is about the upper limit of the microscopic particles and the lower limit of the macroscopic world.

The question now arises as to whether or not there is a sharp boundary between the microscopic and the macroscopic objects? The answer to that question is expected from physicists.

If the three-above quantum "oddities" cannot be applied to macroscopic objects then the question arises: why would de Broglie's theory, as one of the basic theories of quantum physics, be applicable to these objects? We reason that this theory and its equation (1) are not applicable to the macroscopic objects but only to the microscopic particles.

References

{1} S. Kotler, G. A Peterson, E. Shojaee , F. Lecocq, K. Cicak, A. Kwiatkowski , S. Geller, S. Glancy,  E. Knill, R. W. Simmonds, J. Aumentado , J. D. Teufel, Direct observation of deterministic macroscopic entanglement. Science, 372, 622-625 (2021).

{2} Laure Mercier de Lépinay, Caspar F. Ockeloen-Korppi, Matthew J. Woolley, and Mika A. Sillanpää, Quantum mechanics–free subsystem with mechanical oscillators. Science,  372, 625-629 (2021). 

---

[1] We excluded living organisms from macroscopic objects because they are fundamentally different from non-living physical systems.

[2] Hydrogen atoms could appear they be similar because our ability to observe them in detail is rather limited. The same can be said for electrons, protons, neutrons and other microscopic particles.

 

On the Absence of Dark Matter in the Galaxy NGC 1277*

 

On the Absence of Dark Matter in the Galaxy NGC 1277*

Pavle I. Premović

Laboratory for Geochemistry, Cosmochemistry&Astrochemistry,

University of Niš, pavleipremovic@yahoo.com, Niš, Serbia

In science, there are two opposing theories on the origin, development and evolution of the Universe. The naturalistic (atheistic) Big Bang theory states that the Universe began with a “singularity” when all mass, energy, and spacetime was contained in an extremely small particle.[1]

After that event, the universe evolved and expanded according to cosmology, reaching the current state.

Another theistic theory is based on the Bible’s belief that God created the Universe and its galaxies, their stars and planets and other cosmic objects. It also states that the Spirit of God as a divine force is directly involved in the development and evolution of the Universe from its beginning until the present time. During this period His Spirit maintained order in the Universe out of disorder.

The current cosmology estimates that only about 5 % of the galaxy is made of ordinary, or baryonic matter. The rest about 95 % is composed of dark matter. This matter cannot be directly observed since it is composed of non-baryonic matter which does not interact with both baryonic matter and light (and other forms of electromagnetic radiation). Dark matter forms a halo around the galaxy but ordinary matter is mainly situated in its central part where the most of stars dwell.

The evidence for dark matter comes mainly from two sources. The first and most often evidence comes from the rotation curve of the galaxy. Indeed, the current cosmology states that all galaxies behave according to Kepler’s laws. According to his third Law, the rotation of the galaxy, meaning stars in the inner part of the galaxy would orbit much faster than the outer ones. However, observations show that the speed of the outer stars is much higher than the speed of the inner stars. The reason appears to be the presence of dark matter associated with galaxies. Its gravitational effect makes the faster-than-expected orbital speeds of outer stars. The second one arises from the relatively rare strong gravitational lensing of a background galaxy by the massive cluster galaxy.

The current cosmology states that during the history of our Universe, dark matter has guided the galaxy’s formation and evolution. It appears that another role of this matter is that these cosmic processes prevent the galaxy’s disintegration due to its rotation and thus the disintegration of its star systems with their planets. Indeed, the gravitational attraction of this matter keeps stars, dust, and gas together in a galaxy. Moreover, without dark matter, the galaxies in galaxy clusters and in the Universe would fly apart. In other words, dark matter maintains the existence of the galaxy and thus the Universe. Simply speaking no dark matter, no Universe.

It appears that new findings by the research team led by S. Comerón {2} indicate dark matter is absent from the very massive lenticular galaxy NGC 1277.[2] They emphasized that cosmological simulations based on the standard model predict that galaxies with the mass of NGC 1277 should have a dark matter mass fraction of at least 10% and perhaps of up to 70%.

To explain this discrepancy between the observations and the expectation they entertained two possibilities. The first one is that dark matter was stripped by interactions between NGC 1277 and the gravitational field of the cluster of galaxies to which it belongs. The second possibility is that dark matter was expelled from the galaxy when it formed through the merger of small proto-galactic bodies. In their opinion, none of these possibilities is fully acceptable. Comerón and colleagues raised the following intriguing question: how a massive galaxy such as NGC 1277 can form without dark matter? Now other questions arise from this. Is it a more common phenomenon among massive galaxies? If so, are there other massive galaxies in the Universe without dark matter? Is NGC 1277 an exception?

 

According to Wikipedia „NGC 1277“: „its stars being formed during a 100 million year interval about 12 billion years ago“. Of course, we do not know if it still exists, but considering its mass of 17 billion suns, it is reasonable to assume that it has existed for a few billion years. Now another intriguing question arises: how does this galaxy survive without dark matter for billions of years? The origin of NGC 1277 without dark matter and its existence for at least billions of years are until now a cosmological enigma.

 

Within the standard cosmology, there are three possible reasonable explanations for the survival issue of NGC 1277. The first is that Kepler’s laws are not valid for galaxies.[3] The second is that the astronomical estimate of the mass of the ordinary matter of NGC 1277 is incorrect. The third possibility is: that NGC 1277 can be considered a closed system and for survival, it requires some extra unknown energy or force to offset the gravitational effect of dark matter. The source of any these of two is unknown and could be situated outside or inside a galaxy. We leave further considerations of these three possibilities to future research.

Within biblical teaching, one can hypothesize that the God Spirit maintains the survival of NGC 1277. However, if we accept it as a solution, then we are faced with the possibility of appealing to His spirit for the solution of numerous unsolved scientific mysteries. That would be the end of science in general as we know it and with which scientists have been engaged for centuries. But let's not forget that maybe those mysteries are also part of His magnificent creation.

It is written in the Letter Diognetus: "God loved men. For their sake, He made the cosmos and subjected everything on earth to them. To them alone He gave understanding and speech, them alone He allowed to look up to heaven, them alone He formed in His image,...“

References

{1} R. J. Gupta, Testing CCC+TL cosmology with observed baryon acoustic oscillation features. ApJ 55, 964-971 (2024).

{2} S. Comerón, I. Trujillo, M. Cappellari, F. Buitrago, L. E. Garduño, J. Zaragoza-Cardiel, I. A. Zinchenko, M. A. Lara-López, A. Ferré-Mateu, S. Dib, The massive relic galaxy NGC 1277 is dark matter deficient - From dynamical models of integral-field stellar kinematics out to five effective radii. A&A, 20, 1-30 (2023). 

---

*I began to write this paper at the beginning of February 2024. On March 15 this year, Gupta {1} published his work claiming that the Universe contains no dark matter.

[1] Anyway, I called it the primeval God’s particle.

[2] NGC 1277 has mass is several times the mass of the Milky Way and it is an extreme “relic galaxy” or did not interact with any other galaxy.

[3] Of course, these laws are valid for the galaxy stars and their planets.

Relativistic Time Dilation and the Muon Experiment

Relativistic Time Dilation and the Muon Experiment

 

Pavle I. Premović

Laboratory for Geochemistry, Cosmochemistry&Astrochemistry,

University of Niš, pavleipremovic@yahoo.com, Niš, Serbia

Abstract

The time dilation of Lorentz-Einstein can be readily derived from the classical light clock experiment where the clock is positioned perpendicularly to the direction of its motion. The extent of dilation is given by the Lorentz factor: 1/√(1-v²/c²) where v is the relative velocity of the light clock and c is the speed of light.

)

The muon experiment is apparently consistent with this type of time dilation. Assuming that the Lorentz-Einstein time dilation is relevant to the light clock experiment when the clock is aligned along the direction of motion, the Lorentz-Einstein length contraction is usually then derived. However, if there is no such contraction we then deal with a time dilation of the non-Lorentz-Einstein type. The amount of time dilation is now specified by the squared Lorentz factor: 1/(1-v²/c²). It appears that this type of time dilation is even much more agreeable with the muon experimental measurements than the Lorentz-Einstein type. 

Keywords: Special relativity, Lorentz-Einstein, muon, time dilation, time contraction.

1. Introduction

Time dilation and length contraction are two important effects of Special relativity (SR). These two effects depend upon the second postulate of this theory that the speed of light c is the same in all inertial frames of reference [1, 2]. In general, the Lorentz-Einstein (LE) time dilation is a prerequisite for the LE length contraction which only occurs in the direction of motion of the moving frame [1, 2].

To date, several indirect LE length contraction experiments were performed [3 – 9] but no variation in length was measured. Sherwin [10] has reported only one direct experiment and concluded that it was contradictory to the LE length contraction. As far as we are aware there is no critical evaluation and possible revision of his experiment. For many researchers, the LE time dilation is indirectly demonstrated by - muon experiment [1]. Most of the information about this experiment presented in this note is taken from the classic work by Frisch and Smith [7].

According to SR, the proper time ΔT₀ is a time interval of an event measured by an observer in an inertial frame stationary relative to the event. Moreover, the time interval of the same event has a longer duration ΔT, called the improper time, as measured by an observer in an inertial frame moving with a relative speed v to the same event.

The proper length in SR is the length of an object in its rest frame. The improper length is the object's  length in any other frame where moving with a relative speed v.

Many physics textbooks that deal with the concepts of LE time dilation and length contraction depict using a device known as a light clock [1, 2]. In this note, we will especially focus our attention on the time dilation and length contraction when the light clock is positioned along the direction of motion. Of course, you may find all the following derivations in many elementary physics texts.

2. Discusion and Conclusions

The light clock consists of two plane-parallel mirrors M₁ and M₂ facing each other at a distance d apart as in Fig. 1a. I will here consider only the time intervals while a photon moves between mirror M₁ and mirror M₂. The lower mirror M₁ has a light source at the center that emits a photon (or a light signal) at 90 degrees in the direction of mirror M₂. It is usually assumed that the photon reaching mirror M₂ is back-reflected to mirror M₁. Taking into account this assumption, for the light clock at rest the proper time interval is ΔT₀ = 2d/c. However, we must stress here that any photon detection at the mirror M₂ would involve its annihilation.

a

Fig. 1. Measurements and analyses made in different frames. The light clock is positioned perpendicular to the x-axis. (a): No relative motion. (b): light clock moving at speed v.

Now allow the same light clock to be moving with a certain relative speed v horizontally in the direction of the positive x-axis. An observer in the rest frame who is watching this clock could design the following diagram, Fig. 1b. A photon will now travel the larger distance L and thus it will take a longer (improper) time

                                                                 ΔT = 2L/c

According to the LE transformation, ΔT₀ and ΔT are related by the time dilation expression

                                                                ΔT = ΔT₀ /√(1-v²/c²)

where 1/√(1-v²/c²) is the Lorentz or time dilation factor.

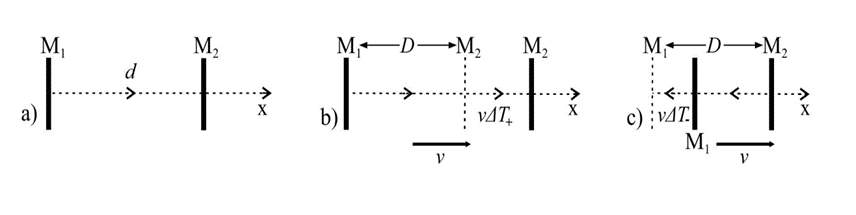
Let us now perform the experiments using the same light clock as in Fig 1a but now aligned along the x-axis, as shown in Fig. 2a. If this clock is resting the time interval is

ΔT₀ = 2d/c.

Fig. 2. Measurements and analysis for the light clock positioned along the x-axis. (a): No relative motion; (b) and (c): the light-clock moving at speed v.

Allow now this clock to move in the direction of the positive x-axis with the speed v, Fig. 2 reach the mirror M₂ the photon will travel the distance

cΔT₊ = D + vΔT₊

in the time interval

                                                                ΔT₊ = D/(c – v)

where D is the length of the light clock measured by a stationary observer.

For  the “back-reflected” photon (Fig. 2c) the time interval 

ΔT_- = D/(c + v)

The total time needed for photon to complete cycle

ΔT = ΔT₊ + ΔT_- = 2cD/(c² -  v²)

Factoring out c² in the denominator

ΔT = 2D/c(1 - v²/c²)

To acquire a relationship between D and d one then invokes the LE time dilation ΔT = ΔT₀ /√1-v²/c²  and then write

2D/c(1 - v²/c²) = 2d/c√(1 - v²/c²)

After simplification, we get the LE length contraction

D = d√(1 - v²/c²)

In this derivation, we hypothesize a priori that the length of the moving light clock is (of course, relativistically) different than the proper length: d ≠ D and the time of this clock is “dilated” relative to the proper time ΔT₀ according to the LE transformation: ΔT = ΔT₀ /√(1-v²/c²). However, there is no experimental evidence corroborating this hypothesis.

Let us assume first that there is no relativistic length contraction i. e., D = d then

                                                                     ΔT = ΔT₀/(1 - v²/c²)

Thus, there is also time dilation but with the squared Lorentz factor 1/(1 - v²/c²) instead 1/√(1 - v²/c²) predicted by LE (hereinafter: the non-LE time dilation). It remains to find out whether the non-LE time dilation agrees with the experiments.

The most convincing experimental evidence for the time dilation in the direction of the motion comes from the cosmic muon experiments. Muons are created in the upper Earth’s atmosphere are secondary products of interactions between primary cosmic rays and the nuclei of atmospheric molecules. Muons travel at relativistic speeds and are unstable particles with a mean lifetime at rest T₀ ~ 2.2 µs. At relativistic speeds, the muons experience time dilation.  This dilation allows them to reach the Earth’s surface before they decay. To measure time dilation, the mean lifetime of muons at rest is compared with the apparent increase in the lifetime of muons in motion using the measurements of their speeds (v/c) and the changes of muon flux with altitude.

The original muon experiment was first done by Rossi & Hall [6] in 1941 who measured muon fluxes at the top of Mt Washington (New England, USA) about 2 km high, and at the base of the mountain. Their experimental results were consistent with the relativistic time dilation. The experiment has since been repeated by several other researchers

.

Let us assume that the muons are moving vertically down from the height of 10 km at the mean speed of 0.98c (= 0.98 × 299,792 km s^-1 = 293,796 km s^-1). Ignoring relativistic effects, they would travel t ~ 34 µs before reaching ground level. The fraction of the muons reaching the ground level is given by

P = 2^-t/T₀ = 2^-34/2.2 = 2.2 × 10^-3 %

Thus, almost no muons could be expected to reach ground level.

In light of the above, the muons moving at a relativistic speed could have a mean lifetime either of T_L = T₀ × 1/√(1 - v²/c²)(LE time dilation) or T_nL= T₀ × 1/(1 - v²/c²) (the non-LE time dilation).  Thus, at the mean speed of 0.98c, the mean lifetime of the muons T could be T_L ~ 11 µs or T_nL ~ 55 µs.  The fraction capable of reaching ground level turns now into

P = 2^-t/T

For the lifetime of T_L ~ 11 µs and T_nL ~ 55 µs this fraction would be about 12 % and 65 %, respectively. Hence, a much larger fraction of the muons (generated in the upper atmosphere) would be capable of reaching ground level in the non-LE case than in the LE. Besides, this much higher prediction is even more consistent with experimental measurements. The question is now how to decide which of these two-time dilations is right.

Let us assume now that there is no time dilation for the moving light clock oriented along the direction of motion (i.e.,  ΔT = ΔT₀). Then it is easy to show that D = d(1 - v²/c²). Thus, there is a length contraction by the non-Lorentz factor.

In conclusion, from the experiment of moving light clock oriented perpendicular to the direction of motion the demonstration of LE time dilation is simple However, there is no way to illustrate the coexisting LE length contraction. On the other hand, there is no way to demonstrate the LE time dilation or length contraction in the case of a moving light clock positioned along the direction of motion without assuming a priori the length change according to the LE transformation. However, for this assumption, there is no experimental evidence.

References

[1] N. D. Mermin, Space and Time in Special Relativity. McGraw-Hill, 1968.

[2] A. Miller, The Principle of Relativity, Albert Einstein's Special Theory of Relativity. Springer, 1998.

[3] D. B. Brace, On double refraction in matter moving through the aether. Phil. Mag., 6, 7, 317-329 (1904).

[4] A. B. Wood, G. A. Tomlinson, L. Essen, The effect of the Fitzgerald-Lorentz contraction on the frequency of longitudinal vibration of a rod. Proc. Royal Soc., 158, 606–633 (1937).

[5] F. T. Trouton and A. O. Rankine, On the electrical resistance of moving matter. Proc. Royal Soc., 80, 420–435 (1908).

[6] B. Rossi B. and Hall D. B. Variation of the rate of decay of mesotrons with momentum. Phys. Rev. 59, 223–228 (1941).

[7] Frisch D. and J. Smith, Measurement of the relativistic time dilation using muons. Am. J. Phys. 31, 342–355 (1963).

[8] J. Bailey, K. Borer, F. Combley, et al., Measurements of relativistic time dilation for positive and negative muons in a circular orbit. Nature 268, 301–305 (1977).

[9] C. Renshaw, Space interferometry mission as a test of Lorentz length contraction. Proc. IEEE Aerospace Conf., 4, 15–24 (1999).

[10] C. W. Sherwin, New experimental test of Lorentz's theory of relativity. Phys. Rev. 35, 3650–3654 (1987).