Relativistic Time Dilation and the Muon Experiment

Relativistic Time Dilation and the Muon Experiment

 

Pavle I. Premović

Laboratory for Geochemistry, Cosmochemistry&Astrochemistry,

University of Niš, pavleipremovic@yahoo.com, Niš, Serbia

Abstract

The time dilation of Lorentz-Einstein can be readily derived from the classical light clock experiment where the clock is positioned perpendicularly to the direction of its motion. The extent of dilation is given by the Lorentz factor: 1/√(1-v²/c²) where v is the relative velocity of the light clock and c is the speed of light.

)

The muon experiment is apparently consistent with this type of time dilation. Assuming that the Lorentz-Einstein time dilation is relevant to the light clock experiment when the clock is aligned along the direction of motion, the Lorentz-Einstein length contraction is usually then derived. However, if there is no such contraction we then deal with a time dilation of the non-Lorentz-Einstein type. The amount of time dilation is now specified by the squared Lorentz factor: 1/(1-v²/c²). It appears that this type of time dilation is even much more agreeable with the muon experimental measurements than the Lorentz-Einstein type. 

Keywords: Special relativity, Lorentz-Einstein, muon, time dilation, time contraction.

1. Introduction

Time dilation and length contraction are two important effects of Special relativity (SR). These two effects depend upon the second postulate of this theory that the speed of light c is the same in all inertial frames of reference [1, 2]. In general, the Lorentz-Einstein (LE) time dilation is a prerequisite for the LE length contraction which only occurs in the direction of motion of the moving frame [1, 2].

To date, several indirect LE length contraction experiments were performed [3 – 9] but no variation in length was measured. Sherwin [10] has reported only one direct experiment and concluded that it was contradictory to the LE length contraction. As far as we are aware there is no critical evaluation and possible revision of his experiment. For many researchers, the LE time dilation is indirectly demonstrated by - muon experiment [1]. Most of the information about this experiment presented in this note is taken from the classic work by Frisch and Smith [7].

According to SR, the proper time ΔT₀ is a time interval of an event measured by an observer in an inertial frame stationary relative to the event. Moreover, the time interval of the same event has a longer duration ΔT, called the improper time, as measured by an observer in an inertial frame moving with a relative speed v to the same event.

The proper length in SR is the length of an object in its rest frame. The improper length is the object's  length in any other frame where moving with a relative speed v.

Many physics textbooks that deal with the concepts of LE time dilation and length contraction depict using a device known as a light clock [1, 2]. In this note, we will especially focus our attention on the time dilation and length contraction when the light clock is positioned along the direction of motion. Of course, you may find all the following derivations in many elementary physics texts.

2. Discusion and Conclusions

The light clock consists of two plane-parallel mirrors M₁ and M₂ facing each other at a distance d apart as in Fig. 1a. I will here consider only the time intervals while a photon moves between mirror M₁ and mirror M₂. The lower mirror M₁ has a light source at the center that emits a photon (or a light signal) at 90 degrees in the direction of mirror M₂. It is usually assumed that the photon reaching mirror M₂ is back-reflected to mirror M₁. Taking into account this assumption, for the light clock at rest the proper time interval is ΔT₀ = 2d/c. However, we must stress here that any photon detection at the mirror M₂ would involve its annihilation.

a

Fig. 1. Measurements and analyses made in different frames. The light clock is positioned perpendicular to the x-axis. (a): No relative motion. (b): light clock moving at speed v.

Now allow the same light clock to be moving with a certain relative speed v horizontally in the direction of the positive x-axis. An observer in the rest frame who is watching this clock could design the following diagram, Fig. 1b. A photon will now travel the larger distance L and thus it will take a longer (improper) time

                                                                 ΔT = 2L/c

According to the LE transformation, ΔT₀ and ΔT are related by the time dilation expression

                                                                ΔT = ΔT₀ /√(1-v²/c²)

where 1/√(1-v²/c²) is the Lorentz or time dilation factor.

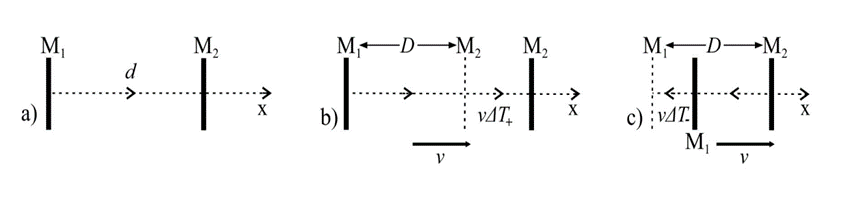
Let us now perform the experiments using the same light clock as in Fig 1a but now aligned along the x-axis, as shown in Fig. 2a. If this clock is resting the time interval is

ΔT₀ = 2d/c.

Fig. 2. Measurements and analysis for the light clock positioned along the x-axis. (a): No relative motion; (b) and (c): the light-clock moving at speed v.

Allow now this clock to move in the direction of the positive x-axis with the speed v, Fig. 2 reach the mirror M₂ the photon will travel the distance

cΔT₊ = D + vΔT₊

in the time interval

                                                                ΔT₊ = D/(c – v)

where D is the length of the light clock measured by a stationary observer.

For  the “back-reflected” photon (Fig. 2c) the time interval 

ΔT_- = D/(c + v)

The total time needed for photon to complete cycle

ΔT = ΔT₊ + ΔT_- = 2cD/(c² -  v²)

Factoring out c² in the denominator

ΔT = 2D/c(1 - v²/c²)

To acquire a relationship between D and d one then invokes the LE time dilation ΔT = ΔT₀ /√1-v²/c²  and then write

2D/c(1 - v²/c²) = 2d/c√(1 - v²/c²)

After simplification, we get the LE length contraction

D = d√(1 - v²/c²)

In this derivation, we hypothesize a priori that the length of the moving light clock is (of course, relativistically) different than the proper length: d ≠ D and the time of this clock is “dilated” relative to the proper time ΔT₀ according to the LE transformation: ΔT = ΔT₀ /√(1-v²/c²). However, there is no experimental evidence corroborating this hypothesis.

Let us assume first that there is no relativistic length contraction i. e., D = d then

                                                                     ΔT = ΔT₀/(1 - v²/c²)

Thus, there is also time dilation but with the squared Lorentz factor 1/(1 - v²/c²) instead 1/√(1 - v²/c²) predicted by LE (hereinafter: the non-LE time dilation). It remains to find out whether the non-LE time dilation agrees with the experiments.

The most convincing experimental evidence for the time dilation in the direction of the motion comes from the cosmic muon experiments. Muons are created in the upper Earth’s atmosphere are secondary products of interactions between primary cosmic rays and the nuclei of atmospheric molecules. Muons travel at relativistic speeds and are unstable particles with a mean lifetime at rest T₀ ~ 2.2 µs. At relativistic speeds, the muons experience time dilation.  This dilation allows them to reach the Earth’s surface before they decay. To measure time dilation, the mean lifetime of muons at rest is compared with the apparent increase in the lifetime of muons in motion using the measurements of their speeds (v/c) and the changes of muon flux with altitude.

The original muon experiment was first done by Rossi & Hall [6] in 1941 who measured muon fluxes at the top of Mt Washington (New England, USA) about 2 km high, and at the base of the mountain. Their experimental results were consistent with the relativistic time dilation. The experiment has since been repeated by several other researchers

.

Let us assume that the muons are moving vertically down from the height of 10 km at the mean speed of 0.98c (= 0.98 × 299,792 km s^-1 = 293,796 km s^-1). Ignoring relativistic effects, they would travel t ~ 34 µs before reaching ground level. The fraction of the muons reaching the ground level is given by

P = 2^-t/T₀ = 2^-34/2.2 = 2.2 × 10^-3 %

Thus, almost no muons could be expected to reach ground level.

In light of the above, the muons moving at a relativistic speed could have a mean lifetime either of T_L = T₀ × 1/√(1 - v²/c²)(LE time dilation) or T_nL= T₀ × 1/(1 - v²/c²) (the non-LE time dilation).  Thus, at the mean speed of 0.98c, the mean lifetime of the muons T could be T_L ~ 11 µs or T_nL ~ 55 µs.  The fraction capable of reaching ground level turns now into

P = 2^-t/T

For the lifetime of T_L ~ 11 µs and T_nL ~ 55 µs this fraction would be about 12 % and 65 %, respectively. Hence, a much larger fraction of the muons (generated in the upper atmosphere) would be capable of reaching ground level in the non-LE case than in the LE. Besides, this much higher prediction is even more consistent with experimental measurements. The question is now how to decide which of these two-time dilations is right.

Let us assume now that there is no time dilation for the moving light clock oriented along the direction of motion (i.e.,  ΔT = ΔT₀). Then it is easy to show that D = d(1 - v²/c²). Thus, there is a length contraction by the non-Lorentz factor.

In conclusion, from the experiment of moving light clock oriented perpendicular to the direction of motion the demonstration of LE time dilation is simple However, there is no way to illustrate the coexisting LE length contraction. On the other hand, there is no way to demonstrate the LE time dilation or length contraction in the case of a moving light clock positioned along the direction of motion without assuming a priori the length change according to the LE transformation. However, for this assumption, there is no experimental evidence.

References

[1] N. D. Mermin, Space and Time in Special Relativity. McGraw-Hill, 1968.

[2] A. Miller, The Principle of Relativity, Albert Einstein's Special Theory of Relativity. Springer, 1998.

[3] D. B. Brace, On double refraction in matter moving through the aether. Phil. Mag., 6, 7, 317-329 (1904).

[4] A. B. Wood, G. A. Tomlinson, L. Essen, The effect of the Fitzgerald-Lorentz contraction on the frequency of longitudinal vibration of a rod. Proc. Royal Soc., 158, 606–633 (1937).

[5] F. T. Trouton and A. O. Rankine, On the electrical resistance of moving matter. Proc. Royal Soc., 80, 420–435 (1908).

[6] B. Rossi B. and Hall D. B. Variation of the rate of decay of mesotrons with momentum. Phys. Rev. 59, 223–228 (1941).

[7] Frisch D. and J. Smith, Measurement of the relativistic time dilation using muons. Am. J. Phys. 31, 342–355 (1963).

[8] J. Bailey, K. Borer, F. Combley, et al., Measurements of relativistic time dilation for positive and negative muons in a circular orbit. Nature 268, 301–305 (1977).

[9] C. Renshaw, Space interferometry mission as a test of Lorentz length contraction. Proc. IEEE Aerospace Conf., 4, 15–24 (1999).

[10] C. W. Sherwin, New experimental test of Lorentz's theory of relativity. Phys. Rev. 35, 3650–3654 (1987).