Hydrogen Molecule in the Light of the de Broglie Theory

 

Hydrogen Molecule in the Light of the de Broglie Theory

Pavle I. Premović

Laboratory for Geochemistry, Cosmochemistry&Astrochemistry,

University of Niš, pavleipremovic@yahoo.com, Niš, Serbia

 In one of the previous communications {1}, we pointed out the discrepancy in the representation of hydrogen molecule (H₂) in chemistry and physics textbooks and its interpretation based on the de Broglie wave theory (duality). According to these textbooks, this molecule consists of two protons and two electrons, each with a charge e, connected by a covalent bond. The experimental equilibrium bond length of H₂ is аbout 7.4 × 10^-11 m or about 43500 diameters of proton (its radius is approximately 0.85 × 10^-15 m).

The de Broglie wave equation for a massive particle in motion is given in the following form 

λ = h/mυ ... (1) 

where λ is the wavelength, h (= 6.63 × 10³⁴ J sec)[1] is Planck's constant and m is the mass of a particle, moving at a speed υ.

If H₂ travels with a non-relativistic speed υ its wavelength is then 

λ(H 2) = h/m(H₂)υ ... (2)   

where m(H₂) is the rest mass of H₂.

The mass of the electron is negligible compared to the mass of proton m(H⁺) then the mass of H₂ m(H₂) ≈ 2m(H⁺) ≈ 3.34 × 10^-27 kg. The most probable/average speed of H₂ which occupies 22.1 dm³ at STP is υ_mp(H₂) ≈ 1500 m sec^-1. Using eqn. (1), a simple calculation shows that its average wavelength λ(H₂) ≈ 1.3 ×10^-10 m is about twice larger than the bond length (аbout 7.4 × 10^-11 m) of H₂.

The wavelength of each proton in this moving H₂ is 

λ(H+) = h/m(H⁺)υ. 

Neglecting again the mass of the electron, we have m(H) = m(H⁺) or m(H⁺) = 1/2 m(H₂). Plugging this last term into eqn. (3) and taking into account eqn. (2) we get 

λ(H⁺) = 2λ(H₂) ... (3).

Using this equation, a simple calculation shows that the average wavelength of the protons in H₂ λ(H⁺) ≈ 2.6 × 10^-10 m.[2] This is four times larger than the bond length of H₂. 

As we pointed out before {1}, the superposition of the waves of these protons can result in two types of interference depending on their phasing. If they are in phase we deal with constructive interference. In this case, the resultant wave would have twice large an amplitude as the proton but its wavelength would be the same as the proton wavelength. If they are out of phase, we deal with the destructive interference, the two proton waves would cancel each other so there would be no resultant wave.

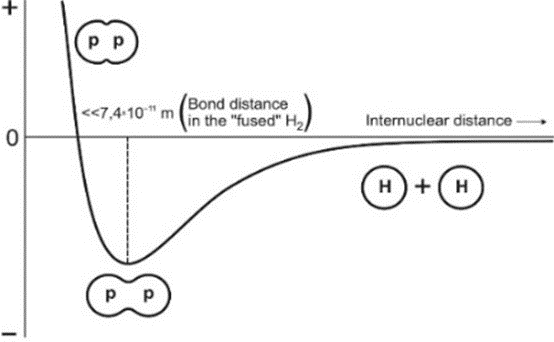
When the protons of H₂ are so far apart (about 43500 proton diameters) one is dealing virtually with two completely separated nuclei. In contrast, de Broglie’s concept would imply that the protons do not exist separately in H₂.[3] Having that in mind and the de Broglie eqn. (1), we speculate, with great hesitation, that the H₂ nucleus is made of two proton nuclei partly “fused” forming the diproton nucleus, H₂²⁺ (or “p-p”). We also hypothesize that H₂²⁺ is dumbbell-shaped, Fig. 2.[4] Its two e = 1+ charges are separated from each other by an internuclear distance much smaller than 7.4 ×10^-11m or << 7.4 × 10^-11 m.[5] At this distance the potential energy of H₂ with the partly “fused” protons is at a minimum, Fig. 1. This distance is the bond length of H₂ with partly “fused” protons.

Fig. 1: Potential energy vs. internuclear distance between two partly “fused” diprotons of H₂.

Fig. 2: Highly exaggerated two-dimensional picture of the (dumbbell shape) partly “fused” diproton nucleus of H₂.

 However, we now face a dilemma: does H₂ consist of two completely separate protons or two protons partly “fused”? This leads to a rather intriguing question: Does the quantum mechanical model of H₂ in motion consist of one wave packet as can be concluded based on the de Broglie model or it consists of two identical wave packets of its protons? Because of its generality, this dilemma can be extended to all diatomic homonuclear molecules gaseous at STP (e. g. the radon molecule: Rn₂) or at non-STP (e. g. the iodine molecule I₂). 

References 

{1} P. I. Premović, The hydrogen molecule and deuterium atom in the light of de Broglie’s theory. The General Science Journal, May 2023. For the sake of clarity, I have modified the first part of a previous version of this communication which refers to de Broglie’s model of H₂.

2} L. Holmlid1 and S. Zeiner-Gundersen, Ultradense protium p(0) and deuterium D(0) and their relation to ordinary Rydberg matter: a review. Phys. Scr. 94 075005 (26pp), 2019.  

---

[1] To avoid confusion in further text, the SI units are given in italics.

[2] Their speed is identical and equal to the speed of H₂. According to eqn. (3), the wavelength of H₂ is twice the wavelength of H⁺.

[3] As far as we are aware, this claim has not been demonstrated experimentally.

[4] In the case of complete fusion, this nucleus would be of a spherical form without the bond length.

[5] It is interesting to note that Holmlid and Zeiner-Gundersen {2} reported the existence of another species of H₂ with bond length 2.3 × 10^-12 m. However, even at this bond length, the protons are very far from each other: about 14,500 proton diameters.